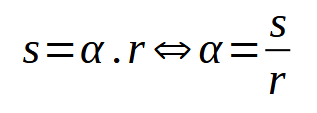A circunferência é, por definição, o lugar geométrico de todos os pontos equidistantes de um ponto central. Ao segmento de reta que une o centro da circunferência a um ponto da circunferência, dá-se o nome de raio (r). E ao segmento de reta que une dois pontos da circunferência e que passa pelo centro, dá-se o nome de diâmetro (d). Disto, conclui-se que d = 2r.
Mas uma coisa intrigava os matemáticos de longa data: como obter o perímetro da circunferência? Para suas tentativas, usavam algo como uma fita métrica, davam uma volta em um objeto circular e anotava esta medida como perímetro. Depois, pegavam o mesmo instrumento e mediam o diâmetro. Para saber a relação entre eles, dividia-se o perímetro pelo diâmetro e chegava-se a medidas cada vez mais próximas de 3,14. É claro que a precisão dos instrumentos interferiam nos resultados e nem sempre se pegava um objeto realmente circular. Então, como abstrair e calcular?
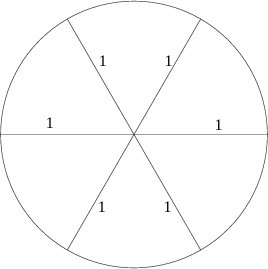
Para tanto, os matemáticos pegaram o desenho de um círculo e dividiam o mesmo em 6 pedaços iguais. Este círculo teria raio igual a 1, para facilitar os cálculos que pudessem seguir.
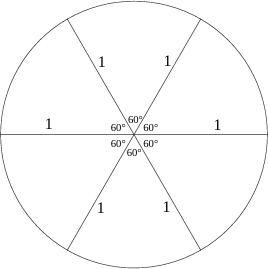
Ajustando estes segmentos para que as aberturas de todos eles tivessem a mesma medida, chegou-se ao ângulo que cada raio teria dos raios adjacentes pois, a soma dos 6 ângulos teria que dar 360°. Para ficar dividido igualmente, cada ângulo deverá ter 60°.
Chama-se de segmento de reta secante ao segmento de reta que toca em dois pontos da circunferência. Observando os raios marcados, traça-se segmentos secantes de modo a formar triângulos entre raios adjacentes. Com isso, forma-se um hexágono dividido em seis triângulos.
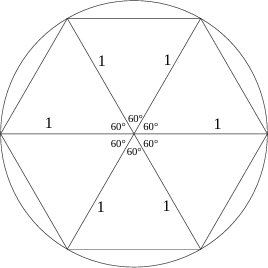
Todos os triângulos apontados são isósceles, ou seja, possuem dois lados com a mesma medida. Da mesma forma, estes triângulos são isoângulos, pois possuem também dois ângulos com a mesma medida. E é possível calcular o seu valor. Para fazer este cálculo, um triângulo terá seus ângulos desconhecidos nomeados como α. Sabe-se que a soma dos ângulos internos de qualquer triângulo resulta em 180°. Assim:
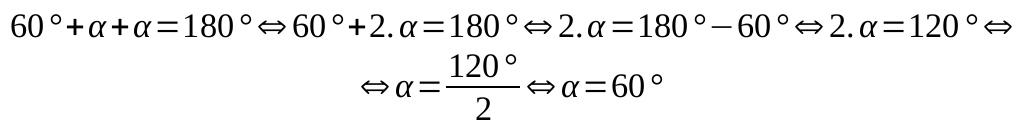
Logo, os ângulos desconhecidos dos triângulos medirão 60°. Portanto, os triângulos marcados são mais que isósceles, são equiláteros, pois se possuem todos os ângulos com a mesma medida, possuirão também os lados com a mesma medida.
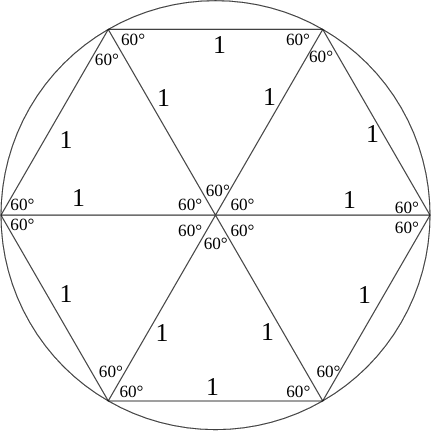
Por um cálculo aproximado, utilizando-se do hexágono como aproximação, tem-se que o comprimento da circunferência valeria 6, pois é um hexágono regular cujo lado mede 1. E se dividir este valor pelo diâmetro, encontra-se o valor de 3.
Ocorre que a circunferência faz curva e a reta é uma aproximação. Pode-se dividir em 12 pedaços para refinar o cálculo e, quanto maior o número de divisões, mais próximo de 3,1415 se chega. Isso quer dizer que se pegasse um fio com 3 comprimentos de raio, ele quase chegaria a dar meia volta na circunferência, faltando aquela parte decimal. Como se usa o comprimento do raio para determinar a medida, criou-se a unidade de ângulo chamada radiano, que representa comprimentos de raio. A unidade foi criada para tratar arcos, mas acaba mostrando uma equivalência melhor com ângulos, de modo que um ângulo de π rad equivale a um ângulo de 180°.
Os cálculos melhoraram e percebe-se que π não é uma dízima periódica e seu número se aproxima de 3,14159265358979…, sem ter um padrão de repetição. Hoje, já se obtém este valor com mais de 1000 casas decimais.
Então, partindo da ideia de que a divisão do perímetro pelo diâmetro se chega ao valor de π, pode-se entender que:
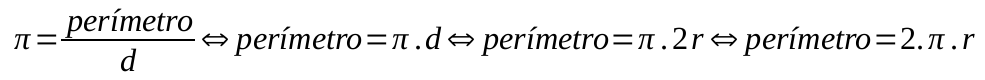
Portanto, a expressão para se calcular o perímetro da circunferência é de 2πr. O interessante é que 2π representa, em radianos, ao ângulo de uma volta completa (360°). Então, caso se deseje obter um ângulo em radianos, pode-se iniciar comparando as equivalências entre graus e radianos.
Colorário
Para se obter o comprimento de um arco (parte da circunferência) será o ângulo em radianos multiplicado pelo raio.
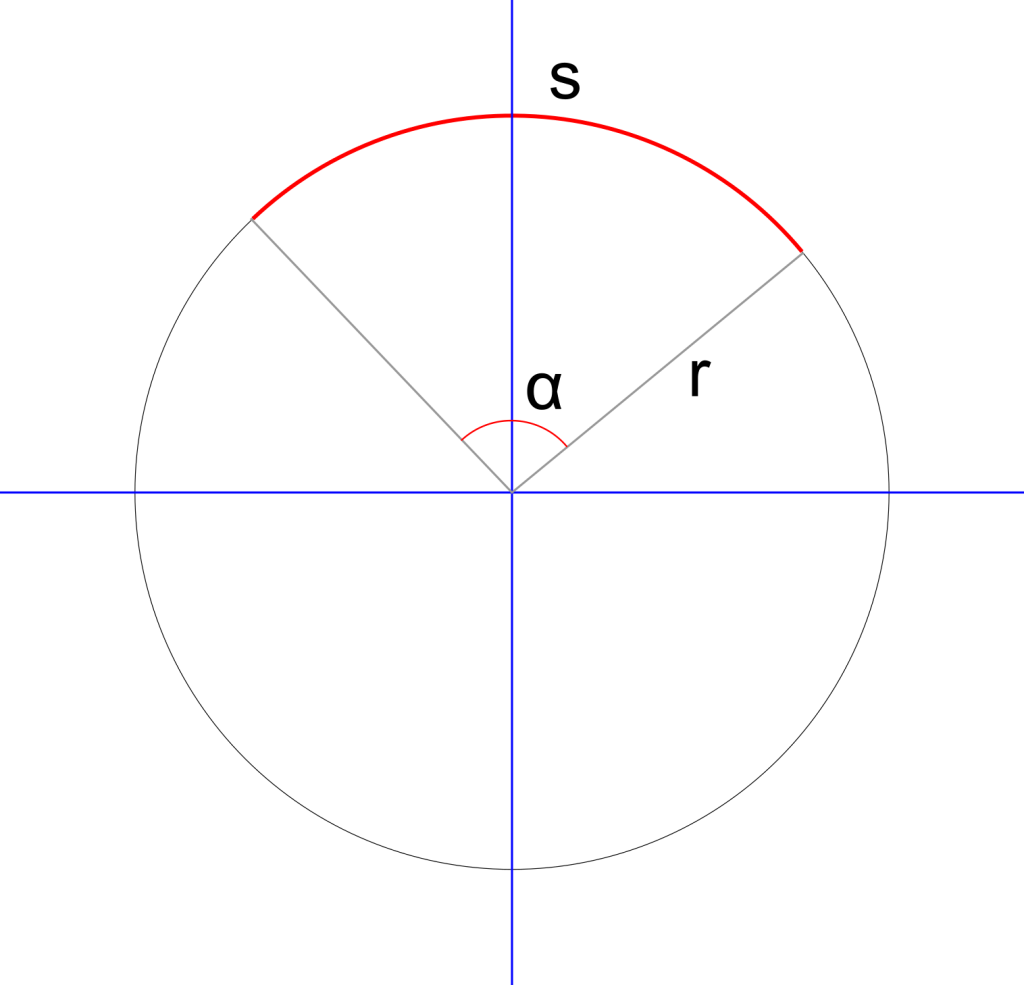
Seja s o comprimento do arco, r o comprimento do raio e α a medida do ângulo em radianos. Pode-se afirmar, conforme visto acima, que: