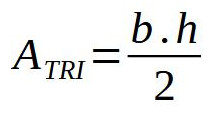Os conceitos matemáticos envolvendo áreas podem ser muito úteis. E a formulação nem é tão complexa, assim. As expressões só são complexas quando não se entende sua origem. Quando a origem é explicada e demonstrada, torna-se mais simples guardá-las. Ou, na pior das hipóteses, demonstrá-las.
Como as expressões possuem uma origem, a ideia aqui é mostrar como se pode obter a área de figuras geométricas, como quadriláteros notáveis e triângulo.
Vale ressaltar que, para o entendimento destas explicações, é necessário a compreensão do que é uma altura e as definições de quadriláteros. Se não dominar estes assuntos, busque-os para construir melhor teus conhecimentos.
Unidade Fundamental de Área
Para se medir áreas, o conceito inicia com uma pequena representação de área, formada por um quadrado. Este quadrado possui os lados com uma unidade de comprimento (1 u.c.), pois pode ser aplicado a qualquer unidade de comprimento, como metro, centímetro, pé, polegada, entre outras. Como não foi definida a unidade, o termo unidade de comprimento é o mais adequado.
Como todos os lados do quadrado são congruentes (possuem a mesma medida), todos os lados medem 1 u.c. e delimitarão uma área com 1 unidade de área (1 u.a.).
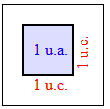
Caso a unidade se comprimento seja metro (m), então a unidade de área será metro quadrado (m2).
Área do Retângulo
Para achar a área do retângulo, ele será dividido em unidades fundamentais de área. Uma vez dividido, pode-se contar a quantidade de unidades fundamentais de área.

Assim, a área do retângulo é calculada como:
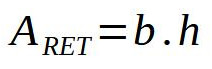
Área do Quadrado
Como o quadrado é um retângulo especial (possui lados adjacentes congruentes), o raciocínio é o mesmo:
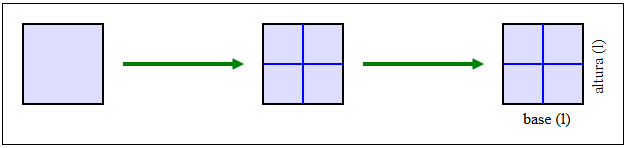
Assim, para calcular sua área, faz-se:
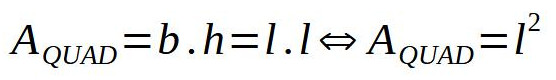
Área do Paralelogramo
Para calcular a área do paralelogramo, por ser uma figura que saiu dos padrões do ângulo reto, a melhor forma para efetuar este cálculo é transformar a figura numa outra já conhecida.
Se traçar a altura num dos vértices obtusos do paralelogramo, aparecerá a figura de um triângulo. Recortando a figura na linha da altura, dá para levar o triângulo para o outro lado. Ao unir novamente as duas figuras, a nova figura formada é um retângulo.

Sendo assim, o cálculo da área do paralelogramo é semelhante à área do retângulo:
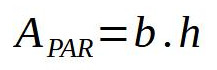
Área do Losango
O losango é um paralelogramo especial, pois possui lados adjacentes congruentes. E nota-se que, ao traçar as duas diagonais, haverá uma diagonal maior (D) e uma diagonal menor (d), formando um ângulo reto entre eles.
Assim como o paralelogramo, a ideia é cortar a figura e transformá-la numa figura já conhecida. Então, ao cortar na linha da diagonal menor, formará dois triângulos. A diagonal maior ficará dividida pela metade em cada triângulo, representando a altura dele. Arrastando um triângulo para se conectar ao outro, pode-se notar que a figura formada é um paralelogramo.
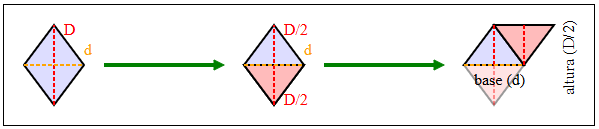
Neste paralelogramo, a base tem o tamanho da diagonal menor (d) e a altura, a metade da diagonal maior (D/2). Assim:
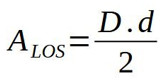
Área do Trapézio
O trapézio é mais desafiador, pois ele é mais irregular que as figuras anteriores. Possui duas bases, caracterizadas pelos lados paralelos, sendo uma base menor (b) e uma base maior (B).
A ideia é semelhante aos exemplos anteriores, mas não temos lados paralelos para unir figuras. Então, pega-se uma figura idêntica e, virando de ponta-cabeça, dá para unir as duas figuras, formando um paralelogramo.

Traçando a altura (h) e percebendo que a base do paralelogramo é a soma das bases do trapézio, dá para se calcular a área do paralelogramo. O trapézio terá a metade desta área, pois o paralelogramo foi formado com 2 trapézios. Assim:
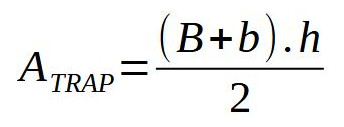
Área do Triângulo
A área do triângulo é semelhante em raciocínio para calcular a área do trapézio. Com uma outra figura do triângulo com as mesmas medidas, basta virá-la de ponta cabeça e juntar os lados, formando um paralelogramo.

Traçando a altura (h) e a base já conhecida (b), a área do paralelogramo formado é obtida. A área do triângulo é a metade desta área, pois é formada com dois triângulos. Assim: