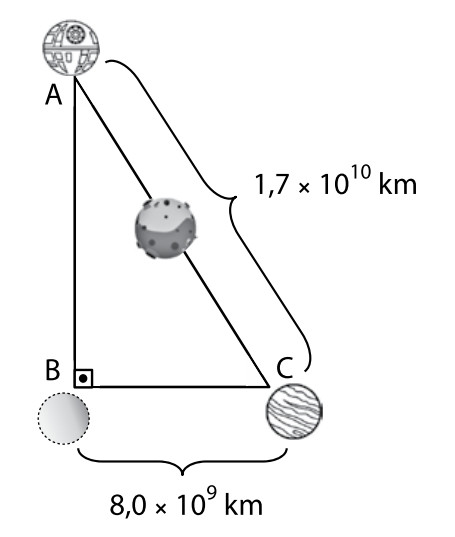
A Estrela da Morte é uma arma ícone da série cinematográfica Star Wars. De formato esférico ela era considerada similar a uma Lua. Essa arma/estação espacial podia se locomover pelo espaço na velocidade da luz, ou seja, 3,0⋅105km/s. Admita que a Estrela da Morte precisasse se posicionar de maneira a realizar um ataque de máxima eficiência ao Planeta C. Inicialmente, a estação espacial encontrava-se no ponto A e, entre ela e o Planeta C, havia um grande asteroide, por isso necessitou ir para o ponto B, de modo a poder visualizar perfeitamente o Planeta C, conforme a figura. Assinale a alternativa que contém o tempo que a Estrela da Morte demorou para se locomover do ponto A para o B.
a)
b)
c)
d)
e) \( \frac { \sqrt {353}}{3} \cdot 10 ^ {4} \text {s} \)
Resolução
Para resolver este exercício, primeiro é necessário saber a distância que a Estrela da Morte vai caminhar, pois a figura formada representa um triângulo retângulo. E, para facilitar, os números que representam distâncias devem estar com potências de 10 iguais. Sendo assim:
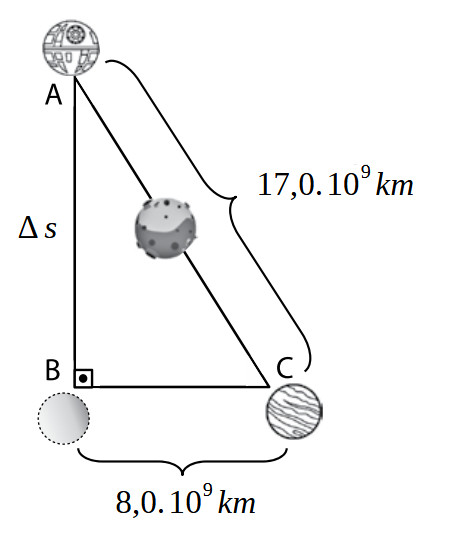
Como os dois números possuem 109 multiplicando, já se sabe que a distância terá o mesmo fator. Então, para efeitos de cálculos, será ignorado e acrescentado ao final. Aplicando o Teorema de Pitágoras:
Agora que já se sabe a distância, e sabendo a velocidade da Estrela da Morte, que é a da luz (3,0.105km/s), basta aplicar a expressão da velocidade média:
Nota: da passagem 3 para a passagem 4, o 15 dá para simplificar por 3, resultando em 5 e divisão de potências com a mesma base (10), conserva a base e subtrai os expoentes (109-5=104).
Resposta: 5,0.104s (A).

Sem comentários